NAEP Assessment Weighting Procedures → Weighting Procedures for the 2012 Assessment → Weighting Procedures for the 2012 Long-Term Trend (LTT) Assessment → Computation of Replicate Weights for Variance Estimation for the 2012 LTT Assessment → Replicate Variance Estimation for the 2012 Long-Term Trend (LTT) Assessment

NAEP Technical DocumentationReplicate Variance Estimation for the 2012 Assessment

Variances for NAEP assessment estimates are computed using the paired jackknife replicate variance procedure. This technique is applicable for common statistics, such as means and ratios, as well as for more complex statistics such as Item Response Theory (IRT) scores.

In general, the paired jackknife replicate variance procedure involves pairing clusters of first-stage sampling units to form H variance strata (h = 1, 2, 3, ...,H) with two units per stratum. The first replicate is formed by deleting one unit at random from the first variance stratum, inflating the weight of the remaining unit to weight up to the variance stratum total, and using all other units from the other (H - 1) strata. This procedure is carried out for each variance stratum resulting in H replicates, each of which provides an estimate of the population total.

The jackknife estimate of the variance for any given statistic is given by the following formula:

                                                where

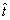•  represents the full sample estimate of the given statistic, and
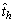•  represents the corresponding estimate for replicate h.

Each replicate undergoes the same weighting procedure as the full sample so that the jackknife variance estimator reflects the contributions to or reductions in variance resulting from the various weighting adjustments. 

The NAEP jackknife variance estimator is based on 62 variance strata resulting in a set of 62 replicate weights assigned to each school and student.

The basic idea of the paired jackknife variance estimator is to create the replicate weights so that use of the jackknife procedure results in an unbiased variance estimator for simple totals and means, which is also reasonably efficient (i.e., has a low variance as a variance estimator). The jackknife variance estimator will then produce a consistent (but not fully unbiased) estimate of variance for (sufficiently smooth) nonlinear functions of total and mean estimates such as ratios, regression coefficients, and so forth (Shao and Tu, 1995).

The development below shows why the NAEP jackknife variance estimator returns an unbiased variance estimator for totals and means, which is the cornerstone to the asymptotic results for nonlinear estimators. See for example Rust (1985). This paper also discusses why this variance estimator is generally efficient (i.e., more reliable than alternative approaches requiring similar computational resources).

The development is done for an estimate of a mean based on a simplified sample design that closely approximates the sample design for first-stage units used in the NAEP studies. The sample design is a stratified random sample with H strata with population weights W_h, stratum sample sizes n_h, and stratum sample means  . The population estimator  and standard unbiased variance estimator  are:

with

The paired jackknife replicate variance estimator assigns one replicate h=1,…, H  to each stratum, so that the number of replicates equals H. In NAEP, the replicates correspond generally to pairs and triplets (with the latter only being used if there are an odd number of sample units within a particular primary stratum generating replicate strata). For pairs, the process of generating replicates can be viewed as taking a simple random sample (J) of size n_h/2 within the replicate stratum, and assigning an increased weight to the sampled elements, and a decreased weight to the unsampled elements. In certain applications, the increased weight is double the full sample weight, while the decreased weight is in fact equal to zero. In this simplified case, this assignment reduces to replacing  with , the latter being the sample mean of the sampled n_h/2 units. Then the replicate estimator corresponding to stratum r is

The r-th term in the sum of squares for  is thus:

In stratified random sampling, when a sample of size n_r/2 is drawn without replacement from a population of size n_r,, the sampling variance is

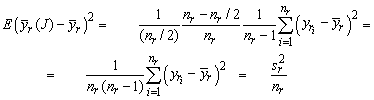
See for example Cochran (1977), Theorem 5.3, using n_r,  as the “population size,” n_r/2 as the “sample size,” and s_r² as the “population variance” in the given formula. Thus,

Taking the expectation over all of these stratified samples of size n_r/2, it is found that

In this sense, the jackknife variance estimator “gives back” the sample variance estimator for means and totals as desired under the theory.

In cases where, rather than doubling the weight of one half of one variance stratum and assigning a zero weight to the other, the weight of one unit is multiplied by a replicate factor of (1+δ), while the other is multiplied by (1- δ), the result is that

In this way, by setting δ equal to the square root of the finite population correction factor, the jackknife variance estimator is able to incorporate a finite population correction factor into the variance estimator.

In practice, variance strata are also grouped to make sure that the number of replicates is not too large (the total number of variance strata is usually 62 for NAEP). The randomization from the original sample distribution guarantees that the sum of squares contributed by each replicate will be close to the target expected value.

For triples, the replicate factors are perturbed to something other than 1.0 for two different replicate factors, rather than just one as in the case of pairs. Again in the simple case where replicate factors that are less than 1 are all set to 0, with the replicate weight factors calculated as follows.

For unit i in variance stratum r

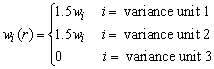
where weight w_i is the full sample base weight.

Furthermore, for r' = r + 31 (mod 62):

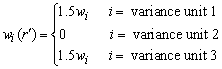
And for all other values r*, other than r and  r´,w_i(r*) = 1.

In the case of stratified random sampling, this formula reduces to replacing  with   for replicate r  and with  for replicate r'.  is the sample mean from a “2/3” sample of 2n_r/3 units from the n_r sample units in the replicate stratum, and  is the sample mean from another overlapping “2/3” sample of 2n_r/3 units from the n_r sample units in the replicate stratum.

The r-th and r´-th replicates can be written as:

From these formulas, expressions for the r-th and r´-th components of the jackknife variance estimator are obtained (ignoring other sums of squares from other grouped components attached to those replicates):

These sums of squares have expectations as follows, using the general formula for sampling variances:

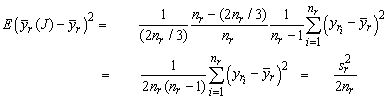
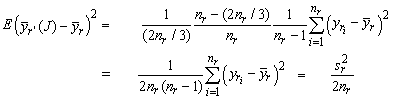
Thus,

as desired again.

Printer-friendly Version