NAEP Technical DocumentationComputation of Replicate Weights for the 2013 Assessment

			Defining Variance Strata and Forming Replicates Computing School-Level Replicate Factors Computing Student-Level Replicate Factors Replicate Variance Estimation

In addition to the full-sample weight, a set of 62 replicate weights was provided for each student. These replicate weights are used in calculating the sampling variance of estimates obtained from the data, using the jackknife repeated replication method. The method of deriving these weights was aimed at reflecting the features of the sample design appropriately for each sample, so that when the jackknife variance estimation procedure is implemented, approximately unbiased estimates of sampling variance are obtained. This section gives the specifics for generating the replicate weights for the 2013 assessment samples. The theory that underlies the jackknife variance estimators used in NAEP studies is discussed in the section Replicate Variance Estimation.

In general, the process of creating jackknife replicate weights takes place at both the school and student level. The precise implementation differs between those samples that involve the selection of Primary Sampling Units (PSUs) and those where the school is the first stage of sampling. The procedure for this second kind of sample also differed starting in 2011 from all previous NAEP assessments. The change that was implemented permitted the introduction of a finite population correction factor at the school sampling stage, developed by Rizzo and Rust (2011). In assessments prior to 2011, this adjustment factor has always been implicitly assumed equal to 1.0, resulting in some overestimation of the sampling variance.

For each sample, the calculation of replicate weighting factors at the school level was conducted in a series of steps. First, each school was assigned to one of 62 variance estimation strata. Then, a random subset of schools in each variance estimation stratum was assigned a replicate factor of between 0 and 1. Next, the remaining subset of schools in the same variance stratum was assigned a complementary replicate factor greater than 1. All schools in the other variance estimation strata were assigned a replicate factor of exactly 1. This process was repeated for each of the 62 variance estimation strata so that 62 distinct replicate factors were assigned to each school in the sample.

This process was then repeated at the student level. Here, each individual sampled student was assigned to one of 62 variance estimation strata, and 62 replicate factors with values either between 0 and 1, greater than 1, or exactly equal to 1 were assigned to each student.

For example, consider a single hypothetical student. For replicate 37, that student’s student replicate factor might be 0.8, while for the school to which the student belongs, for replicate 37, the school replicate factor might be 1.6. Of course, for a given student, for most replicates, either the student replicate factor, the school replicate factor, or (usually) both, is equal to 1.0.

A replicate weight was calculated for each student, for each of the 62 replicates, using weighting procedures similar to those used for the  full-sample weight. Each replicate weight contains the school and student replicate factors described above. By repeating the various weighting procedures on each set of replicates, the impact of these procedures on the sampling variance of an estimate is appropriately reflected in the variance estimate.

Each of the 62 replicate weights for student k in school s in stratum j can be expressed as follows: 

 

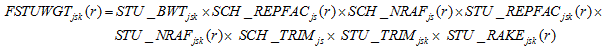
• STU_BWT_jsk  is the student base weight;

• SCH_REPFAC_js(r) is the school-level replicate factor for replicate r;

• SCH_NRAF_js(r) is the school-level nonresponse adjustment factor for replicate r;

• STU_REPFAC_jsk(r) is the student-level replicate factor for replicate r;

• STU_NRAF_jsk(r) is the student-level nonresponse adjustment factor for replicate r;

• SCH_TRIM_js is the school-level weight trimming adjustment factor;

• STU_TRIM_jsk is the student-level weight trimming adjustment factor; and

• STU_RAKE_jsk(r) is the student-level raking adjustment factor for replicate r.

Specific school and student nonresponse and student-level raking adjustment factors were calculated separately for each replicate, thus the use of the index (r), and applied to the replicate student base weights. Computing separate nonresponse and raking adjustment factors for each replicate allows resulting variances from the use of the final student replicate weights to reflect components of variance due to these various weight adjustments.

School and student weight trimming adjustments were not replicated, that is, not calculated separately for each replicate. Instead, each replicate used the school and student trimming adjustment factors derived for the full sample. Statistical theory for replicating trimming adjustments under the jackknife approach has not been developed in the literature. Due to the absence of a statistical framework, and since relatively few school and student weights in NAEP require trimming, the weight trimming adjustments were not replicated.

Printer-friendly Version