Table of Contents  |  Search Technical Documentation  |  References

NAEP Analysis and Scaling → Summary Statistics for Scale Scores of Groups → Procedures for Estimating Group Scale Score Statistics and Their Variances → Using Plausible Values to Estimate the Proportions of Variance Explained by Student Sampling and Measurement Error

NAEP Technical DocumentationUsing Plausible Values to Estimate the Proportions of Variance Explained by Student Sampling and Measurement Error

It is possible to partition the estimation error variance of a statistic using the variance components needed to estimate the total error variance of the statistic of interest. Using plausible values, the final estimate of the variance of the statistic, t^* , is the sum of two components

where the average sampling variance over the M sets of plausible values, which approximates the uncertainty due to sampling respondents is

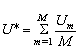
(this is approximated in NAEP by U₁, the variance computed from the first set of plausible values), and where the variance among the M estimates , which approximates the between-estimate variance is

The quantity (1 + M ^–1)B is the estimate of variance due to the latency of . So, the proportion of error variance due to sampling students from the population is U*/V, and the proportion due to the latent nature of θ is (1 + M ^–1)B/V. The value of U^*/V roughly corresponds to reliability in classical test theory and indicates the amount of information about an average individual's θ present in the observed responses of the individual. It should be recalled again that the objective of NAEP is not to estimate and compare values of individual examinees, the accuracy of which is gauged by reliability coefficients. The objective of NAEP, rather, is to estimate population and subpopulation characteristics, and the marginal estimation methods described above have been designed to do so consistently regardless of the values of reliability coefficients.

NAEP has studied the proportion of variance due to sampling and due to the latent nature of θ for subject area scales and composites for the populations as a whole and for selected subpopulations. The proportion of variance due to the latency of θ for the populations as a whole varies somewhat among subject areas, tending to be largest for the long-term trend writing assessment, where there is low correlation between tasks and each student responded to only one or at most two tasks. The proportion of variance due to latency of θ is smallest for the composites of the national main assessment subjects with several scales, where the number of items per student is largest. Essentially, the variance due to the latent nature of θ is largest when there is less information about a student's scale score. Given fixed assessment time, this decrease in information will occur whenever the amount of information per unit time decreases as can happen when many short constructed-response or multiple-choice items are replaced by a few extended constructed-response items. Note that there is a distinction between estimation error variance of an estimate of a statistic (such as the mean of the distribution) and the estimate of the variance of the θ distribution. The former depends on the accuracy of measurement; the large-sample model-based expected value of the latter does not.

Printer-friendly Version