- Surveys & Programs
- Data & Tools
- Fast Facts
- News & Events
- Publications & Products
- About Us
Table of Contents | Search Technical Documentation | References
NAEP Technical DocumentationOverlap Control of Twelfth-Grade School Sample With the Education Longitudinal Study
The Education Longitudinal Study (ELS) was another study which was conducted in U.S. schools with a twelfth grade. In order to minimize burden on schools, the sample was designed to minimize the overlap between the NAEP 2002 sample and the ELS sample. This is done using a technique explicated below called 'Keyfitzing', named after the original paper's author (Keyfitz (1951)).
The twelfth-grade public school sample has as unconditional probabilities of selection the values ![]() equal to min(1,Es), where Es is the expected number of 'hits' as computed in School Selection for Twelfth-Grade Public Schools. The procedure (a modification of that proposed by Keyfitz (1951)) is designed to assure that these desired values are in fact the unconditional probabilities, while making the conditional probabilities higher if the school is not in the ELS sample, and lower if the school is in the ELS sample.
equal to min(1,Es), where Es is the expected number of 'hits' as computed in School Selection for Twelfth-Grade Public Schools. The procedure (a modification of that proposed by Keyfitz (1951)) is designed to assure that these desired values are in fact the unconditional probabilities, while making the conditional probabilities higher if the school is not in the ELS sample, and lower if the school is in the ELS sample.
Let N denote the set of schools which we will sample into the NAEP sample and E the set of schools that were sampled in the ELS sample. Let ![]() be the probability that school s is in the ELS sample (determined by the ELS sample design).
be the probability that school s is in the ELS sample (determined by the ELS sample design).
Using general probability theory regarding conditional probabilities, the selection probability of a school in the NAEP twelfth grade public school sample can be written as
![]()
The overlap between NAEP and ELS can be made small by setting ![]() where possible. For schools with
where possible. For schools with ![]() that are in the ELS sample,
that are in the ELS sample, ![]() is set to 0, (i.e., such schools are given no chance of selection in NAEP). Assigning them a conditional selection probability of 0 does this:
is set to 0, (i.e., such schools are given no chance of selection in NAEP). Assigning them a conditional selection probability of 0 does this:
![]()
Schools with ![]() , which are not in the ELS sample, receive a conditional selection probability of
, which are not in the ELS sample, receive a conditional selection probability of
![]()
Note that under the condition ![]() , this is a well-defined probability (between 0 and 1). To a school with
, this is a well-defined probability (between 0 and 1). To a school with ![]() that was in the ELS sample, the algorithm assigns
that was in the ELS sample, the algorithm assigns
![]()
Note again that this is a well-defined probability (between 0 and 1) under the condition ![]() . A school with
. A school with ![]() that was not in the ELS sample gets
that was not in the ELS sample gets
![]()
These formulas define the conditional probability in entering the NAEP sample in all cases. It can easily be shown that the conditional probabilities assigned in this way are consistent with the unconditional probabilities desired. In the first case, the unconditional selection probability in NAEP of a school with ![]() is
is
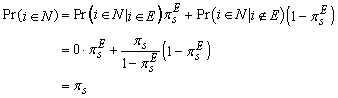
as desired. In the second case, for a school with ![]() , we have
, we have
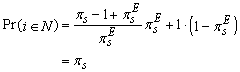
also as desired.
A final step in the process is to take care of schools which were certainty selections and had expected multiple hits (Es ≥1 ). These have a conditional probability of 1, and are also assigned a conditional hits expected value of Es, so that they can receive multiple hits in the conditional sample as well (in other words, the expected hits values of unconditional certainty schools are unaffected by the Keyfitzing process).
Last updated 08 July 2008 (PE)