NAEP Technical DocumentationComputation of Measures of Size

There were five objectives underlying the process for determining the probability of selection for each school and for setting the number of students to be sampled within each selected school:

• to meet the target student sample size for each grade;
• to select an equal-probability sample of students;
• to limit the number of students selected from any one school;
• to ensure that the sample within a school does not include a very high percentage of the students in the school, unless all students are included; and
• to reduce the rate of sampling of small schools, in recognition of the greater cost and burden per student of conducting assessments in such schools.

The goal in determining the school's measure of size is to optimize across the last four objectives in terms of maintaining the precision of estimates and the cost effectiveness of the sample design. The following algorithm was used to assign a measure of size to each school based on its estimated grade-specific enrollment. The computation of the measure of size for grade 12 differed from that for grades 4 and 8. 

In the formulas below, x_js refers to the estimated grade enrollment for private school type j and school s, and P_s is a PSU weight associated with the PSS area sample.

For fourth and eighth grade, the preliminary measures of size (MOS) were set as follows:

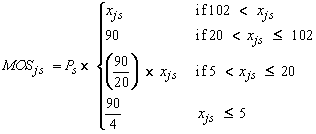
And for twelfth grade:

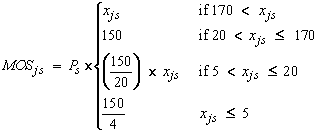
The preliminary school measure of size was rescaled to create an expected number of hits by applying a multiplicative constant b_j, which varies by grade and school type. The private school sample design allowed multiple “hits.” For example, a school with two hits will have twice as many students sampled as a single-hit school, and three hits, three times, etc. To limit respondent burden, constraints were placed on the number of hits allowed per school. For grade 4 it was one hit, for grade 8 it was two, and for grade 12, three.

It follows that the final measure of size, E_js, was defined as:

where u_j  is the maximum number of hits allowed.

The school's probability of selection π_js was given by:

 π_js = min(E_js,1)

One can choose a value of b_j such that the expected overall student sample yield matches the desired targets specified by the design, where the expected yield is calculated by summing the product of an individual school’s probability and its student sample yield across all schools in the frame.

In addition, new- and newly-eligible-schools were sampled from the new-school frame. The assigned measures of size for these schools,

                                                ,

used the b_j and u_j values from the main school sample for the grade and school type (i.e., the same sampling rates as for the main school sample).

The variable  is the probability of selection of the diocese into the new-school diocese (d) sample.

Printer-friendly Version